導入
今日は、Pythonと機械学習を駆使して、最新の日の株価の終値と初値の差を予測する方法についてお話ししましょう。このアプローチでは、Ridge回帰という強力な機械学習アルゴリズムを使用しています。まず、データの処理から始め、Ridge回帰の基本と実装、最後に得られた結果の評価について説明します。
データの準備と前処理
分析の第一歩は、株価データを適切に準備し、前処理することです。Pythonのpandasライブラリを使用して株価データを読み込み、必要な変換を行いました。特に、株価の上昇額を計算し、日付ごとにデータを整理しました。目的変数は最新の日の株価上昇率で、特徴量はそれ以前の日の株価上昇率です。
Ridge回帰モデルの訓練
Ridge回帰は、過学習を防ぎながらモデルの精度を向上させるために使用されます。この分析では、異なるalpha値(0.01, 0.1, 1, 10, 100)でモデルを訓練しました。alphaは正則化の強度を制御し、大きな値ほど強い正則化が適用されます。交差検証を用いて、それぞれのalphaに対する平均二乗誤差(MSE)とR2スコアを計算しました。
結果と評価
結果は以下の通りです:
- Alpha: 0.01 – Mean MSE: 54644.72, Mean R2: -0.2468
- Alpha: 0.1 – Mean MSE: 54644.72, Mean R2: -0.2468
- Alpha: 1 – Mean MSE: 54644.70, Mean R2: -0.2468
- Alpha: 10 – Mean MSE: 54644.51, Mean R2: -0.2468
- Alpha: 100 – Mean MSE: 54642.64, Mean R2: -0.2468
残念ながら、これらの結果はモデルの性能が低いことを示しています。R2スコアが0未満であることから、モデルがデータをほとんど説明できていないことがわかります。alphaの値を変えても、性能に大きな差は見られませんでした。
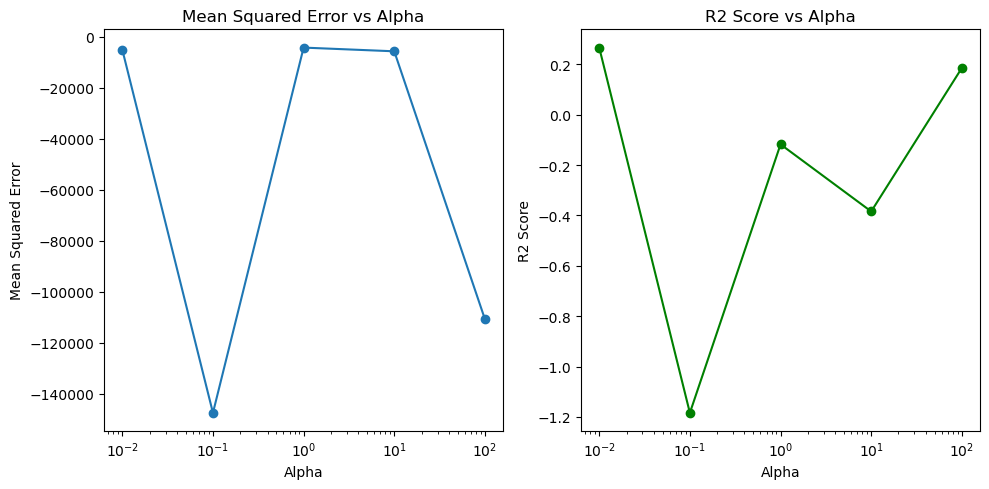
この結果から、私たちはモデルのアプローチを見直す必要があることが分かります。もっと複雑なモデルを試すか、データの特徴量をより詳細に分析することが次のステップとなるでしょう。
まとめ
Ridge回帰は株価予測において有望なアプローチですが、今回の結果は期待に満たないものでした。しかし、機械学習は試行錯誤の過程です。今回の経験から学び、より良いモデルを構築することができるでしょう。興味深い分析の旅を共有できて嬉しく思います。次回のブログで新たな発見をお届けできることを楽しみにしています!
コード
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.impute import SimpleImputer
import numpy as np
import seaborn as sns
# CSVファイルをDataFrameとして読み込む
csv_file = 'stock_data.csv'
stock_hist_df = pd.read_csv(csv_file)
# 株価上昇額を計算
stock_hist_df['price_increase'] = stock_hist_df['close_price'] - stock_hist_df['open_price']
# 日付を日付型に変換(必要に応じて)
stock_hist_df['date'] = pd.to_datetime(stock_hist_df['date'])
# コード毎にグループ化して、各日付の株価上昇率を列にする
pivot_df = stock_hist_df.pivot_table(index='code', columns='date', values='price_increase')
pivot_df.head() # データフレームの最初の数行を表示
# 最新の日付を特定
latest_date = pivot_df.columns.max()
# 目的変数 y (最新の日付の株価上昇率) と特徴量 X (それ以外の日付の株価上昇率)
y = pivot_df[latest_date]
X = pivot_df.drop(columns=[latest_date])
# yのNaN値を含む行を削除
X = X[y.notna()]
y = y[y.notna()]
# 欠損値の処理(Xの特徴量のみ)
imputer = SimpleImputer(strategy='mean')
X_imputed = imputer.fit_transform(X)
# データを訓練セットとテストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X_imputed, y, test_size=0.2, random_state=0)
# alpha値のリスト
alphas = [0.01, 0.1, 1, 10, 100]
# それぞれのalphaについて交差検証を実行
for alpha in alphas:
model = Ridge(alpha=alpha)
# 交差検証を用いて、平均MSEとR2スコアを計算
mse_scores = cross_val_score(model, X_imputed, y, scoring='neg_mean_squared_error', cv=5)
r2_scores = cross_val_score(model, X_imputed, y, scoring='r2', cv=5)
mean_mse = -np.mean(mse_scores)
mean_r2 = np.mean(r2_scores)
print(f'Alpha: {alpha} - Mean MSE: {mean_mse}, Mean R2: {mean_r2}')
# MSEのプロット
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.plot(alphas, mse_scores, marker='o')
plt.title('Mean Squared Error vs Alpha')
plt.xlabel('Alpha')
plt.ylabel('Mean Squared Error')
plt.xscale('log')
# R2スコアのプロット
plt.subplot(1, 2, 2)
plt.plot(alphas, r2_scores, marker='o', color='green')
plt.title('R2 Score vs Alpha')
plt.xlabel('Alpha')
plt.ylabel('R2 Score')
plt.xscale('log')
plt.tight_layout()
plt.show()