今回は、株の高値と初値の上昇が1%以上であったかを予測するために、ロジスティック回帰モデルとハイパーパラメータチューニングを利用する方法について話していきます。
1. データ準備と前処理
まず最初に、株価データを扱いやすい形に整える必要があります。このプロセスには、データの読み込み、特定の日付のデータ抽出、および必要な計算を行うステップが含まれます。例えば、’2024-01-26’の高値と初値の上昇率を計算し、1%以上の上昇があったかどうかをフラグとして記録します。このようにして、データをモデルが学習しやすい形に整えることが重要です。
2. モデル構築とハイパーパラメータチューニング
ロジスティック回帰モデルは、特定のイベントが起きる確率を予測するのに非常に適しています。しかし、モデルの性能を最大限に引き出すためには、正則化の強さや最適化問題の解法といったハイパーパラメータの調整が欠かせません。グリッドサーチとランダムサーチはこのプロセスを自動化し、最適なパラメータセットを見つけ出すのに役立ちます。このステップでは、実際にこれらの方法を用いて、モデルの精度を向上させる試みを行います。
3. 結果の評価と解釈
モデルを訓練し、最適なハイパーパラメータを見つけた後は、テストデータを用いてその性能を評価します。ROC曲線やAUCスコア、混同行列などの指標は、モデルがどれだけうまく機能しているかを理解するのに役立ちます。これらの結果から、モデルの強みと弱点を洞察し、さらなる改善の余地を探ることができます。
結果の評価
グリッドサーチとランダムサーチの結果を比較すると、モデルの性能、実行時間、そして最適なパラメータに関して興味深い違いが見られます。それぞれの結果を以下の点で評価します。
実行時間
- グリッドサーチは1055.17秒(約17.5分)を要しました。これは、指定された全てのハイパーパラメータの組み合わせを網羅的に試すため、時間がかかります。
- ランダムサーチはわずか55.50秒と、グリッドサーチに比べて大幅に短い時間で完了しました。ランダムサーチはパラメータ空間からランダムに組み合わせを選択するため、より少ない計算リソースで済みます。
最適なパラメータ
- グリッドサーチで見つかった最適なパラメータは
{'logreg__C': 0.01, 'logreg__penalty': 'l1', 'logreg__solver': 'liblinear'}でした。これは正則化が強く適用される設定で、モデルの複雑さを抑えることを意味します。 - ランダムサーチでは、
{'logreg__solver': 'saga', 'logreg__penalty': 'none', 'logreg__C': 0.1}が最適なパラメータとして選ばれました。この設定では正則化が適用されていないため、モデルがデータに対してより柔軟にフィットする可能性があります。
モデルの性能
グリッドサーチのAUCスコアは0.632と、一定の予測能力を持っているものの、改善の余地がある結果でした。混同行列と分類レポートからは、ポジティブクラスの識別能力が非常に低いことが明らかになりました。
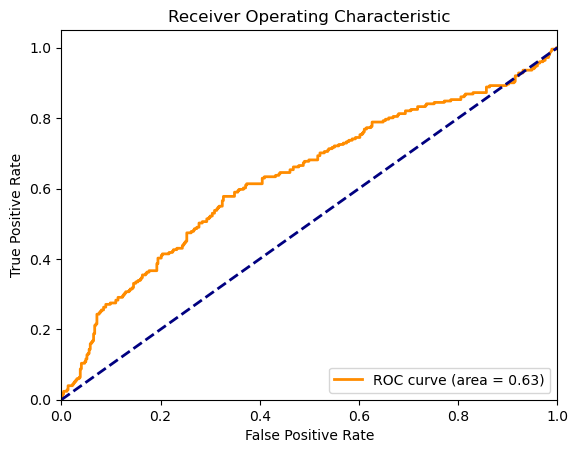
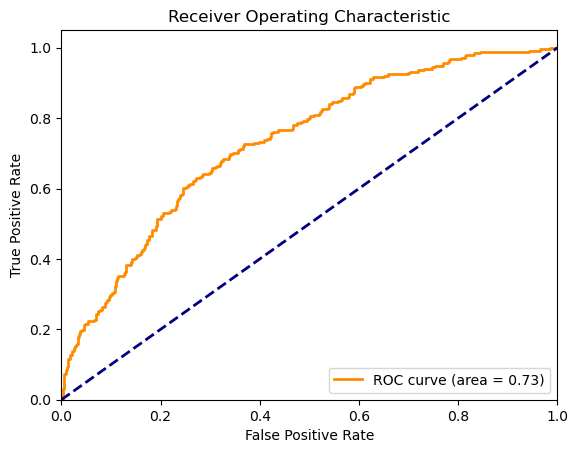
ランダムサーチのAUCスコアは0.733と、グリッドサーチの結果よりも明らかに改善されています。ポジティブクラスの識別能力に関しても、リコールと精度が向上しており、よりバランスの取れたモデルとなっています。
結論
- ランダムサーチは、計算コストが大幅に低いにも関わらず、グリッドサーチよりも優れた性能を示しました。これは、ハイパーパラメータの探索においてランダムサーチが非常に効率的であることを示しています。
- ランダムサーチで得られたモデルは、特にAUCスコアの向上とポジティブクラスの識別能力の改善が顕著でした。これは、パラメータ空間内でのランダムな探索が、未探索のがら空き地域において良好なパラメータ組み合わせを見つけ出す可能性を示唆しています。
- どちらもPresionで最適解を求めた結果、グリッドサーチはすべてのパラメターを網羅的にテストしてしますので、Presicionだけ見るとグリッドサーチの方が結果がよくなってしまっています。
コード
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score,roc_curve, auc, roc_auc_score, confusion_matrix, classification_report
from sklearn.model_selection import train_test_split, GridSearchCV, RandomizedSearchCV
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# CSVファイルをDataFrameとして読み込む
csv_file = 'stock_data.csv'
stock_hist_df = pd.read_csv(csv_file)
# '2024-01-26'のデータを抽出
specific_date_df = stock_hist_df[stock_hist_df['date'] == '2024-01-26']
# open_priceに対するhigh_priceの上昇率を計算
specific_date_df['increase_flag'] = ((specific_date_df['high_price'] - specific_date_df['open_price']) / specific_date_df['open_price'] >= 0.01).astype(int)
# codeをインデックスとするDataFrameを作成
result_df = specific_date_df.set_index('code')['increase_flag']
result_df.info()
# 株価上昇額を計算
stock_hist_df['price_increase'] = stock_hist_df['high_price'] - stock_hist_df['open_price']
# 日付を日付型に変換(必要に応じて)
stock_hist_df['date'] = pd.to_datetime(stock_hist_df['date'])
# コード毎にグループ化して、各日付の株価上昇率を列にする
pivot_df = stock_hist_df.pivot_table(index='code', columns='date', values='price_increase')
pivot_df.head() # データフレームの最初の数行を表示
# result_df と pivot_df を code を基に結合
merged_df = pd.merge(result_df.reset_index(), pivot_df.reset_index(), on='code', how='inner')
merged_df = merged_df.drop(columns=pd.to_datetime("2024-01-26"))
merged_df = merged_df.dropna()
# ターゲット列と特徴量列を分離
X = merged_df.drop(columns=['increase_flag']) # ここで'target'はターゲット列の名前
y = merged_df['increase_flag']
# 訓練セットとテストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 特徴量DataFrameの列名をすべて文字列型に変換
X_train.columns = X_train.columns.astype(str)
X_test.columns = X_test.columns.astype(str)
# グリッドサーチの開始時刻を記録
start_time = time.time()
# データの標準化とロジスティック回帰モデルを含むパイプラインを作成
pipeline = Pipeline([
('scaler', StandardScaler()),
('logreg', LogisticRegression(max_iter=1000))
])
# 探索したいハイパーパラメータの範囲を指定
param_grid = {
'logreg__C': [0.01, 0.1, 1, 10, 100], # 正則化の強さ
'logreg__penalty': ['l1', 'l2', 'elasticnet', 'none'], # 正則化の種類
'logreg__solver': ['newton-cg', 'lbfgs', 'liblinear', 'sag', 'saga'] # 最適化問題の解法
}
# 注意: すべてのsolverがすべてのpenaltyタイプをサポートしているわけではありません。
# 'liblinear' は 'l1' と 'l2' をサポートします。
# 'saga' は 'elasticnet' をサポートします。
# 'lbfgs', 'newton-cg', 'sag' は 'l2' または 'none' をサポートします。
# GridSearchCVオブジェクトを作成
grid_search = GridSearchCV(pipeline, param_grid, cv=5, scoring='precision', verbose=3)
# 訓練データセットでフィットさせる
grid_search.fit(X_train, y_train)
# グリッドサーチの終了時刻を記録
end_time = time.time()
# かかった時間を計算
elapsed_time = end_time - start_time
# グリッドサーチの経過時間を出力
print(f"GridSearchCV took {elapsed_time:.2f} seconds")
# 最適なパラメータとスコアを表示
print(f'Best parameters: {grid_search.best_params_}')
print(f'Best cross-validation score: {grid_search.best_score_}')
# テストデータセットでのスコアを評価
test_score = grid_search.score(X_test, y_test)
print(f'Test set score: {test_score}')
# 最適なパラメータでモデルを再設定
best_params = grid_search.best_params_
model = LogisticRegression(C=best_params['logreg__C'],penalty=best_params['logreg__penalty'],solver=best_params['logreg__solver'])
# パイプラインに再設定(標準化を含む)
pipeline = Pipeline([
('scaler', StandardScaler()),
('logreg', model)
])
# 訓練データでモデルを訓練
pipeline.fit(X_train, y_train)
# テストデータに対する予測確率を取得
y_score = pipeline.predict_proba(X_test)[:, 1]
# ROCカーブとAUCスコアの計算
fpr, tpr, thresholds = roc_curve(y_test, y_score)
roc_auc = auc(fpr, tpr)
# ROCカーブの描画
plt.figure()
plt.plot(fpr, tpr, color='darkorange', lw=2, label='ROC curve (area = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic')
plt.legend(loc="lower right")
plt.show()
# AUCスコアの表示
print(f'AUC Score: {roc_auc_score(y_test, y_score)}')
# 混同行列と分類レポートの出力
y_pred = pipeline.predict(X_test)
print('Confusion Matrix:')
print(confusion_matrix(y_test, y_pred))
print('\nClassification Report:')
print(classification_report(y_test, y_pred))
# ランダムサーチの開始時刻を記録
start_time = time.time()
# データの標準化とロジスティック回帰モデルを含むパイプラインを作成
pipeline = Pipeline([
('scaler', StandardScaler()),
('logreg', LogisticRegression(max_iter=1000))
])
# 探索したいハイパーパラメータの範囲を指定
param_grid = {
'logreg__C': [0.01, 0.1, 1, 10, 100], # 正則化の強さ
'logreg__penalty': ['l1', 'l2', 'elasticnet', 'none'], # 正則化の種類
'logreg__solver': ['newton-cg', 'lbfgs', 'liblinear', 'sag', 'saga'] # 最適化問題の解法
}
# 注意: すべてのsolverがすべてのpenaltyタイプをサポートしているわけではありません。
# 'liblinear' は 'l1' と 'l2' をサポートします。
# 'saga' は 'elasticnet' をサポートします。
# 'lbfgs', 'newton-cg', 'sag' は 'l2' または 'none' をサポートします。
# ランダムサーチCVオブジェクトを作成
randomized_search = RandomizedSearchCV(pipeline, param_grid, cv=5, scoring='precision', verbose=3)
# 訓練データセットでフィットさせる
randomized_search.fit(X_train, y_train)
# ランダムサーチの終了時刻を記録
end_time = time.time()
# かかった時間を計算
elapsed_time = end_time - start_time
# ランダムサーチの経過時間を出力
print(f"GridSearchCV took {elapsed_time:.2f} seconds")
# 最適なパラメータとスコアを表示
print(f'Best parameters: {randomized_search.best_params_}')
print(f'Best cross-validation score: {randomized_search.best_score_}')
# テストデータセットでのスコアを評価
test_score = randomized_search.score(X_test, y_test)
print(f'Test set score: {test_score}')
# 最適なパラメータでモデルを再設定
best_params = randomized_search.best_params_
model = LogisticRegression(C=best_params['logreg__C'],penalty=best_params['logreg__penalty'],solver=best_params['logreg__solver'])
# パイプラインに再設定(標準化を含む)
pipeline = Pipeline([
('scaler', StandardScaler()),
('logreg', model)
])
# 訓練データでモデルを訓練
pipeline.fit(X_train, y_train)
# テストデータに対する予測確率を取得
y_score = pipeline.predict_proba(X_test)[:, 1]
# ROCカーブとAUCスコアの計算
fpr, tpr, thresholds = roc_curve(y_test, y_score)
roc_auc = auc(fpr, tpr)
# ROCカーブの描画
plt.figure()
plt.plot(fpr, tpr, color='darkorange', lw=2, label='ROC curve (area = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic')
plt.legend(loc="lower right")
plt.show()
# AUCスコアの表示
print(f'AUC Score: {roc_auc_score(y_test, y_score)}')
# 混同行列と分類レポートの出力
y_pred = pipeline.predict(X_test)
print('Confusion Matrix:')
print(confusion_matrix(y_test, y_pred))
print('\nClassification Report:')
print(classification_report(y_test, y_pred))