こんにちは、株式市場の未来を予測の第一歩を踏み出してみた。!
株式市場って不確実で予測が難しいですよね。プロフェッショナルがいろいろとやっているので、そんな簡単にうまくいくわけないとは思っているものの機械学習の勉強を兼ねて、初めて見た。
今回は、K-近傍法(K-NN)を使って、株価が上がるかどうかを予測してみましょう!
データの準備からスタート
まずは、株価データを拾ってくるところからスタート。今回は、こちらのファイルを利用した。まずはこれをパソコンに取り込みます。銘柄ごとに株価の動きや取引量を計算して、最新日の株価が1%以上上がるかどうか(これを1か0で表します)を見ていきます。
K-NNモデルで予測してみよう
データをトレーニング用とテスト用に分けて、K-NNモデルを作ってみた。ここで大事なのは、「kの値」です。この値によって予測の仕方が変わるみたい。
結果をグラフでチェック
予測の「当たりやすさ」(精度)や「見逃さない度」(再現率)、「正確さ」(適合率)をグラフにしてみましょう。これで、どのkの値が一番いいかが分かります。結果をグラフでチェック
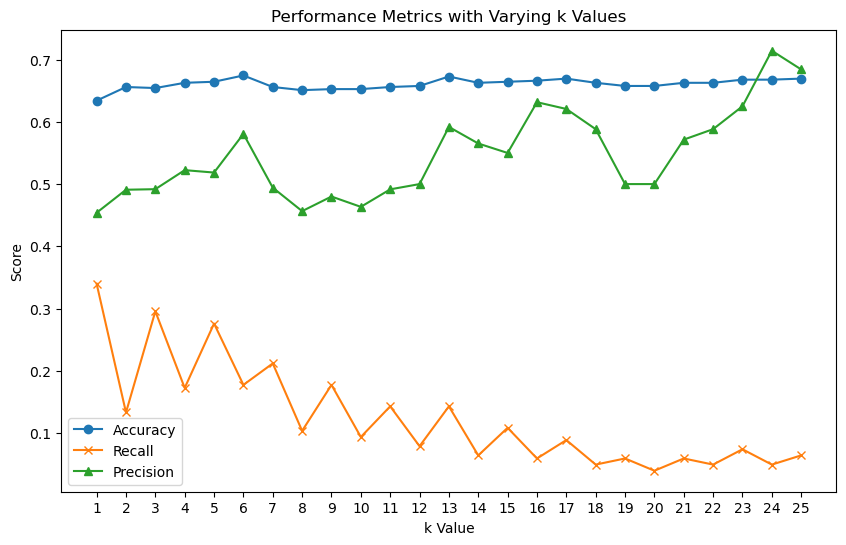
混同行列とROC曲線で深堀り
上記の結果からkを6にして深堀してみた。
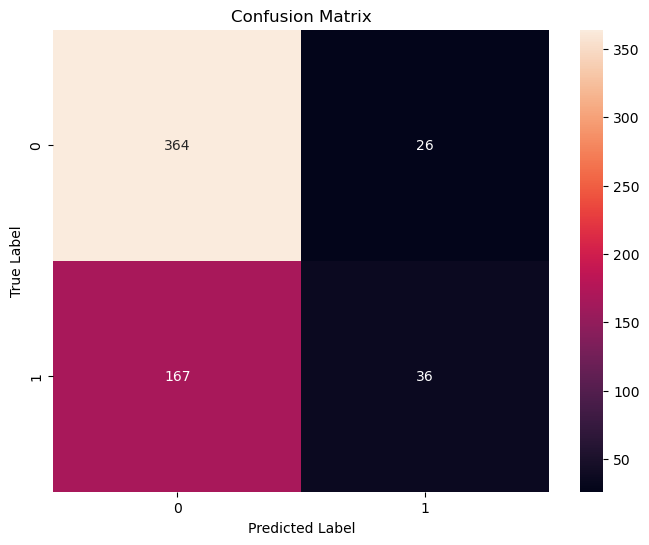
混同行列っていうのは、予測がどれくらい当たってるかを示す表で、今回の結果は以下のような感じ
- 「株価が上がらない(0)」の予測精度(適合率)は69%、再現率は93%で、F1スコアは79%です。
- 「株価が上がる(1)」の予測精度は58%、再現率は18%で、F1スコアは27%です。
- 全体の精度(accuracy)は67%です。
- 「株価が上がらない(0)」の予測が比較的良好:適合率が高いことは、モデルが「株価が上がらない」と予測した場合、その予測が正しい可能性が高いことを意味します。再現率も高いので、実際に株価が上がらないケースの多くを捉えています。
- 「株価が上がる(1)」の予測が改善の余地あり:こちらの適合率は低めで、再現率はさらに低いです。これは、モデルが「株価が上がる」と予測する際にはあまり自信がなく、実際に株価が上がるケースの多くを見逃していることを示しています。
- 全体の精度は67%:これは、全予測のうち正しいものの割合ですが、特に「株価が上がる」予測の改善が全体の精度向上につながるでしょう。
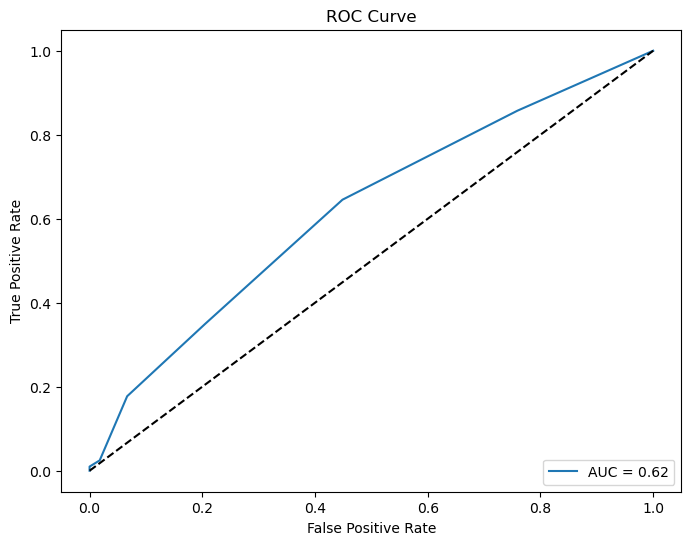
このROC(Receiver Operating Characteristic)曲線は、モデルの分類性能を評価するために用いられるグラフで、真陽性率(True Positive Rate, TPR)と偽陽性率(False Positive Rate, FPR)の関係をプロットしているそうです。AUC(Area Under the Curve)はROC曲線の下の領域の面積で、モデルがランダムな予測よりどれだけ優れているかを示す指標のようです。
このグラフにおけるAUCの値は0.62になっています。AUCのスケールは0から1までで、1に近いほどモデルの性能が良いことを意味し、0.5はランダムな推測の性能を示します。したがって、AUCが0.62であることは、モデルがランダムな推測よりは優れているものの、まだ改善の余地があることを示していりようです。
最後に
K-近傍法は始めるのにいい方法だけど、初めからうまくいくわけないですね。
投資はリスクが伴いますが、データ分析を通じて、そのリスクを少しでも減らすことができるかもしれないのと、目的は、機械学習の勉強なので、少しずつ学んで行けたらと思います。
コード
使用したコードは以下の通り
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score, recall_score, precision_score, classification_report, confusion_matrix, roc_curve, auc
import seaborn as sns
# CSVファイルをDataFrameとして読み込む
csv_file = 'stock_data.csv'
stock_hist_df = pd.read_csv(csv_file)
# ユニークな日付の数を数える
X = stock_hist_df['date'].nunique()
# 日付でソート
stock_hist_df = stock_hist_df.sort_values(by='date')
# 各codeとnameごとにグループ化し、必要な計算を行う
def calculate_metrics(group):
group = group.sort_values(by='date', ascending=False)
metrics = {}
metrics['code'] = group['code'].iloc[0]
# n日前のデータを計算する関数
def calc_day_ago_metrics(n):
if len(group) > n:
metrics[f"{n}day_ago_raise"] = group['high_price'].iloc[n] - group['open_price'].iloc[n]
metrics[f"{n}day_raise_rate"] = metrics[f"{n}day_ago_raise"] / group['open_price'].iloc[n] if group['open_price'].iloc[n] != 0 else None
metrics[f"{n}day_volume"] = group['volume'].iloc[n]
else:
metrics[f"{n}day_ago_raise"] = None
metrics[f"{n}day_raise_rate"] = None
metrics[f"{n}day_volume"] = None
# 最新日とそれ以前の日々について計算
for n in range(0, X): # Xはユニークな日付の数
calc_day_ago_metrics(n)
return pd.Series(metrics)
# 新しいデータフレームを生成
aggregated_df = stock_hist_df.groupby(['code',]).apply(calculate_metrics).reset_index(drop=True)
# '0day_raise_rate'が0.01以上の場合は1、それ以外の場合は0をセット
aggregated_df['result'] = aggregated_df['0day_raise_rate'].apply(lambda x: 1 if x >= 0.01 else 0)
# 指定された列を削除
aggregated_df = aggregated_df.drop(columns=['0day_ago_raise', '0day_raise_rate', '0day_volume','code'])
# 指定された列を削除
aggregated_df = aggregated_df.drop(columns=['0day_ago_raise', '0day_raise_rate', '0day_volume','code'])
# NaNを含む行を削除
aggregated_df = aggregated_df.dropna()
# 特徴量とターゲット変数を分ける
X = aggregated_df.drop('result', axis=1)
y = aggregated_df['result']
# データをトレーニングセットとテストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 異なるkの値に対する指標を記録するためのリスト
k_values = range(1, 26)
accuracies = []
recalls = []
precisions = []
# 各kについてモデルをトレーニングし、指標を評価
for k in k_values:
knn = KNeighborsClassifier(n_neighbors=k)
knn.fit(X_train, y_train)
y_pred = knn.predict(X_test)
accuracies.append(accuracy_score(y_test, y_pred))
recalls.append(recall_score(y_test, y_pred))
precisions.append(precision_score(y_test, y_pred))
# 指標をグラフにプロット
plt.figure(figsize=(10, 6))
plt.plot(k_values, accuracies, marker='o', label='Accuracy')
plt.plot(k_values, recalls, marker='x', label='Recall')
plt.plot(k_values, precisions, marker='^', label='Precision')
plt.xlabel('k Value')
plt.ylabel('Score')
plt.title('Performance Metrics with Varying k Values')
plt.xticks(k_values)
plt.legend()
plt.show()
# テストデータに対する予測
knn = KNeighborsClassifier(n_neighbors=6)
knn.fit(X_train, y_train)
y_pred = knn.predict(X_test)
# 精度、再現率、適合率、F1スコアを計算して表示
print("Classification Report:")
print(classification_report(y_test, y_pred))
# 混同行列を計算
cm = confusion_matrix(y_test, y_pred)
# 混同行列を表示
plt.figure(figsize=(8, 6))
sns.heatmap(cm, annot=True, fmt="d")
plt.title("Confusion Matrix")
plt.xlabel("Predicted Label")
plt.ylabel("True Label")
plt.show()
# ROC曲線とAUCスコアの計算
y_pred_prob = knn.predict_proba(X_test)[:, 1]
fpr, tpr, thresholds = roc_curve(y_test, y_pred_prob)
roc_auc = auc(fpr, tpr)
# ROC曲線をプロット
plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, label=f'AUC = {roc_auc:.2f}')
plt.plot([0, 1], [0, 1], 'k--') # 50%の線
plt.title('ROC Curve')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.legend(loc="lower right")
plt.show()