今日は、Lasso回帰を使った株価予測の面白い分析についてお話しします。データサイエンスが株式市場の謎を解き明かす鍵となるかもしれませんよ!
はじめに:Lasso回帰って何?
Lasso回帰は、線形回帰の一種で、特に「特徴量選択」に優れています。これは、データの中から最も重要な情報を選び出して、予測モデルを作る手法です。私たちはこの手法を使って、株価の終値と初値の差を予測しようとしました。
分析の流れ
- データの準備:まず、株価データを読み込み、各銘柄の日ごとの株価上昇額を計算しました。
- 特徴量の設定:次に、最新の日の株価上昇額を予測するために、それ以前の日のデータを特徴量として使用しました。
- Lasso回帰の適用:異なるalpha値(正則化の強さを制御するパラメータ)を試しながら、Lasso回帰モデルを訓練しました。
結果の分析
Alpha: 0.01 – Mean MSE: 61902.206518338004, Mean R2: -0.35281913869130277
Alpha: 0.1 – Mean MSE: 61783.26874215723, Mean R2: -0.34963839924895973
Alpha: 1 – Mean MSE: 60825.595166476865, Mean R2: -0.3211916112590815
Alpha: 10 – Mean MSE: 50755.11164860657, Mean R2: -0.08971933508685988
Alpha: 100 – Mean MSE: 41513.47363058019, Mean R2: 0.15608155642135024
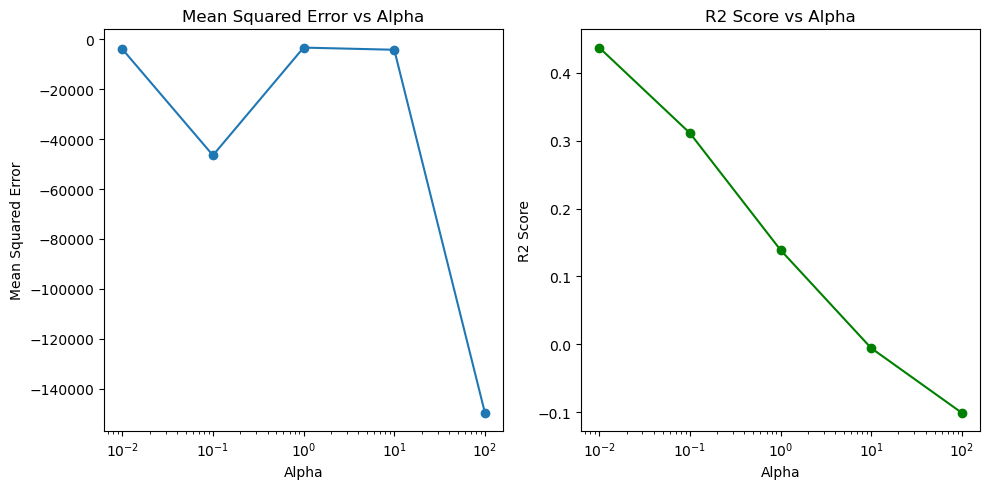
結果は上記の通り、とても興味深いものでした。alpha値を0.01から100まで変化させたところ、Mean MSE(平均平方二乗誤差)とMean R2(決定係数)が大きく変動しました。特に、alphaが100のときには、Mean MSEが最小となり、Mean R2が0.156で、最も良い結果を示しました。
特徴量の重要性とは?
Lasso回帰モデルでは、特定の特徴量が予測結果にどれだけ影響を与えているかを理解することが重要です。私たちが作成した図は、これらの特徴量の重要性を視覚的に示しています。
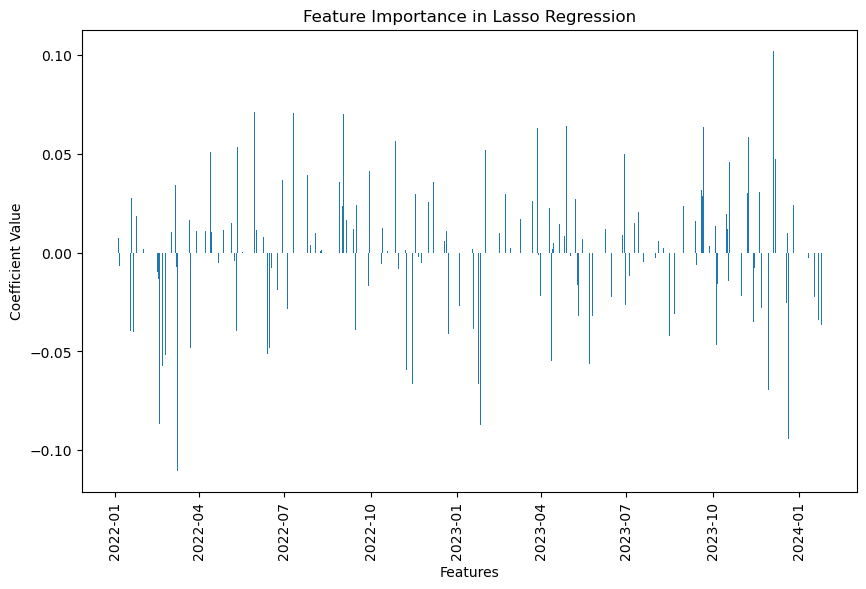
- 係数のバー図:各特徴量(この場合は、異なる日付の株価上昇額)に対応する係数の値を棒グラフで示しています。この係数は、特徴量が目的変数(最新の日の株価上昇額)に与える影響の大きさを表しています。
- 係数の値:係数の値が大きいほど、その特徴量は予測に大きな影響を与えていることを意味します。逆に、係数が0または非常に小さい場合、その特徴量は予測にほとんど寄与していないと考えられます。
- 特徴量の選択:Lasso回帰の特徴は、不要な特徴量(予測にほとんど貢献しない特徴量)の係数を0に近づけることで、モデルを単純化し、過学習を防ぐことにあります。この方法により、最も重要な特徴量だけが選ばれます。
結果の意味
- Mean MSEの低下:MSEが低いほど、モデルの予測誤差が小さいことを意味します。つまり、alphaが高いほど、予測の精度が向上していることになります。
- Mean R2の向上:R2スコアが正の値を取ると、モデルがデータのバリエーションをある程度説明していることを意味します。こちらもalphaが高くなるにつれて改善されています。
最後に
この分析は、株価予測にLasso回帰を適用する一例です。データサイエンスは、複雑な株式市場の動きを理解するための強力なツールであり、さらに探求する価値があります。ただし、実際の投資にこれを適用する際は、市場の変動やその他の要因も考慮に入れる必要があります。
データサイエンスと株式投資の交差点で、さらなる発見が待っています!次回のブログでも、このような興味深い分析を紹介していきますので、お楽しみに!
コード
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import Lasso
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.impute import SimpleImputer
import numpy as np
import seaborn as sns
# CSVファイルをDataFrameとして読み込む
csv_file = 'stock_data.csv'
stock_hist_df = pd.read_csv(csv_file)
# 株価上昇額を計算
stock_hist_df['price_increase'] = stock_hist_df['close_price'] - stock_hist_df['open_price']
# 日付を日付型に変換(必要に応じて)
stock_hist_df['date'] = pd.to_datetime(stock_hist_df['date'])
# コード毎にグループ化して、各日付の株価上昇率を列にする
pivot_df = stock_hist_df.pivot_table(index='code', columns='date', values='price_increase')
pivot_df.head() # データフレームの最初の数行を表示
# 最新の日付を特定
latest_date = pivot_df.columns.max()
# 目的変数 y (最新の日付の株価上昇率) と特徴量 X (それ以外の日付の株価上昇率)
y = pivot_df[latest_date]
X = pivot_df.drop(columns=[latest_date])
# yのNaN値を含む行を削除
X = X[y.notna()]
y = y[y.notna()]
# 欠損値の処理
imputer = SimpleImputer(strategy='mean')
X_imputed = imputer.fit_transform(X)
# データを訓練セットとテストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X_imputed, y, test_size=0.2, random_state=0)
# alpha値のリスト
alphas = [0.01, 0.1, 1, 10, 100]
# それぞれのalphaについて交差検証を実行
for alpha in alphas:
model = Lasso(alpha=alpha)
# 交差検証を用いて、平均MSEとR2スコアを計算
mse_scores = cross_val_score(model, X_imputed, y, scoring='neg_mean_squared_error', cv=5)
r2_scores = cross_val_score(model, X_imputed, y, scoring='r2', cv=5)
mean_mse = -np.mean(mse_scores)
mean_r2 = np.mean(r2_scores)
print(f'Alpha: {alpha} - Mean MSE: {mean_mse}, Mean R2: {mean_r2}')
# MSEのプロット
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.plot(alphas, mse_scores, marker='o')
plt.title('Mean Squared Error vs Alpha')
plt.xlabel('Alpha')
plt.ylabel('Mean Squared Error')
plt.xscale('log')
# R2スコアのプロット
plt.subplot(1, 2, 2)
plt.plot(alphas, r2_scores, marker='o', color='green')
plt.title('R2 Score vs Alpha')
plt.xlabel('Alpha')
plt.ylabel('R2 Score')
plt.xscale('log')
plt.tight_layout()
plt.show()
# 最適なalpha値でLasso回帰モデルを訓練
alpha_optimal = 100
lasso = Lasso(alpha=alpha_optimal)
lasso.fit(X_train, y_train)
# 各特徴量の係数を取得
coefficients = lasso.coef_
# 特徴量の名前を取得(pivot_dfから日付の列名を除く)
feature_names = pivot_df.drop(columns=[latest_date]).columns
# 係数の絶対値に基づいて特徴量をプロット
plt.figure(figsize=(10, 6))
plt.bar(feature_names, coefficients)
plt.xticks(rotation=90) # X軸のラベルを90度回転
plt.xlabel('Features')
plt.ylabel('Coefficient Value')
plt.title('Feature Importance in Lasso Regression')
plt.show()
