今日は、株価の動きを予測する一つの興味深い方法についてお話ししようと思います。それは、Pythonと線形回帰モデルを使って、株の終値と始値の差を推定する方法です。データサイエンスと株式投資の世界がどのように交差するか、見てみましょう!
データの準備:株価データの読み込みから始めよう
まず最初に、Pythonを使って株価データを読み込みます。今回は、CSVファイルから株価データを読み込んで、Pandasのデータフレームに変換しました。そして、各株式の終値と始値の差を計算し、これを株価上昇額として新しい列に追加しました。さらに、データを日付型に変換して、分析に適した形に整理しました。
モデルの訓練:線形回帰で未来を予測?
次に、最新の日付の株価上昇率を目的変数とし、それ以前の日付のデータを特徴量として線形回帰モデルを訓練しました。欠損値は平均値で補完し、データを訓練セットとテストセットに分割しています。ここがデータサイエンスの魔法が働くところです!
結果の評価:予測はどのくらい正確?
さて、肝心のモデルの性能ですが、R2スコア(決定係数)は-1.2885、MSE(平均二乗誤差)は11002.3830でした。これらの数値は、正直言ってあまり良い結果ではありません。R2スコアがマイナスというのは、モデルがデータのパターンを全く捉えられていないことを意味します。株価の動きは非常に予測が難しく、多くの外部要因に影響されるため、このような結果になることも珍しくありません。
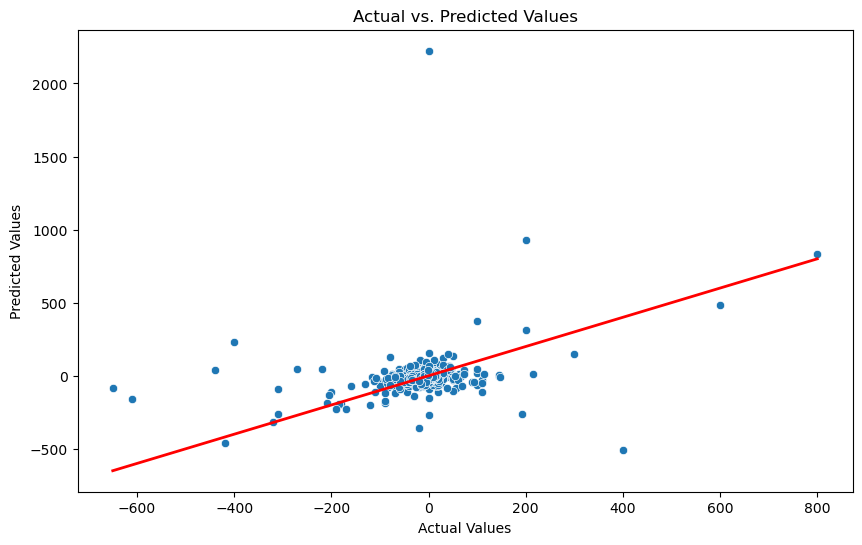
データサイエンスと株式市場の難しさ
この実験からわかることは、株式市場は非常に複雑で予測が難しいということです。線形回帰モデルは基本的なツールであり、より複雑なモデルや追加のデータを用いることで、より良い予測ができるかもしれません。しかし、株式市場に完璧な予測モデルは存在しないことを忘れてはなりません。投資は自己責任で、データ分析はその一助となることを期待しましょう。
それでは、次回のブログでまたお会いしましょう!データサイエンスと株式投資の面白い旅は続きます!
コード
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.impute import SimpleImputer
from sklearn.model_selection import train_test_split
import seaborn as sns
# CSVファイルをDataFrameとして読み込む
csv_file = 'stock_data.csv'
stock_hist_df = pd.read_csv(csv_file)
# 株価上昇額を計算
stock_hist_df['price_increase'] = stock_hist_df['close_price'] - stock_hist_df['open_price']
# 日付を日付型に変換(必要に応じて)
stock_hist_df['date'] = pd.to_datetime(stock_hist_df['date'])
# コード毎にグループ化して、各日付の株価上昇率を列にする
pivot_df = stock_hist_df.pivot_table(index='code', columns='date', values='price_increase')
# 最新の日付を特定
latest_date = pivot_df.columns.max()
# 目的変数 y (最新の日付の株価上昇率) と特徴量 X (それ以外の日付の株価上昇率)
y = pivot_df[latest_date]
X = pivot_df.drop(columns=[latest_date])
# yのNaN値を含む行を削除
X = X[y.notna()]
y = y[y.notna()]
# 欠損値の処理(Xの特徴量のみ)
imputer = SimpleImputer(strategy='mean')
X_imputed = imputer.fit_transform(X)
# データを訓練セットとテストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X_imputed, y, test_size=0.2, random_state=0)
# 線形回帰モデルの訓練
model = LinearRegression()
model.fit(X_train, y_train)
# テストデータで予測
y_pred = model.predict(X_test)
# 性能評価
r2 = r2_score(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)
print(f'R2 Score: {r2}')
print(f'MSE: {mse}')
